Alright I guess I should actually let you folks know what's going on with this.
I'm not sure if I intend to continue, but I have felt zero drive to post about math for the past few months, and I think it is better to just sit on that than to force myself to turn out posts that I feel are low quality and uninformative. I kinda feel like I'm spinning my wheels here and not actually being helpful at all.
So hiatus is extended to be indefinite.
I do want to pick this back up at some future point, but probably not anytime real soon.
20 July 2011
01 May 2011
Takin' a break
So it's crunch time for school and I think it would probably be best if I took a 2-3 week hiatus from this blog to concentrate on actually doing my linear algebra work.
Back after finals.
Back after finals.
25 April 2011
I can't identify with zero
Another case of forgetting to write a post beforehand. Whoops. Spring Break is bad for productivity. Gonna have to put off graphing again (see, it's a post that will require work). Let's talk about something interesting and conceptual instead.
Identities! Also, zero. I'm going to explain why you can't divide by zero.
An identity is a number that, when processed through an operation with another number, gives you that other number. That sounds confusing. It isn't, really. You already know this, you just don't have a name for it.
The multiplicative identity is 1. x*1 = x, you see. It doesn't change the value of what you're multiplying it with. This is important because remember, you can write 1 as anything over itself. So 1 being an identity allows you to re-write equations and put them into a different form. Pretty cool!
The additive identity is 0, because x+0 = x. This one also lets you re-write equations. You use it constantly in simple algebra while solving for x. x+3 = 7, subtract 3 from both sides, x + 3 - 3 = 7-3; x + 0 = 4. You're using the fact that adding zero doesn't change the answer to figure out the solution to the problem.
Yeah, yeah, this is stuff you already know, but nobody sat down and bothered to explain what it meant, I'm certain. I didn't find out about identities as a THING until linear algebra, when you start using this thing called an identity MATRIX. You multiply it with a matrix and get the original matrix. UNSURPRISINGLY it's an idea that comes from more basic math concepts which are never adequately explained!
I mean, you can say it's obvious that x+0 = x, but why? Why is that obvious? Math operates on the methods we use to define it. Did you know that x0 is 1? Yeah, something times itself 0 times is equal to 1. Why? Because if it wasn't, the rest of our math wouldn't make sense. (Speaking of, the exponential identity is also 1.)
So we created this thing called an identity and defined it the way we did because it helps us solve problems.
This is only tangentially related to identities, but it's a good place to talk about zero. Why can't you divide by zero? We know from doing limits that division by zero goes to infinity. It's not finite, but the limit exists. Well, the fact that it's not finite is important. That means that x/0 doesn't actually have a value. You can't say it equals infinity, because infinity is a concept, not a number.
You can also explain it algebraically. I'll even bust out the code for this one.
So what's
if the top makes it 0 and the bottom makes it infinite? We don't know. There's no way to reconcile that. It's undefined. The answer there doesn't exist.
Unlike all other numbers, 0 does not have an inverse that turns it into 1. x*1/x = 1, but 0*1/0 ≠ 1 because 0/0 is not defined and it's definitely not equal to 1. And that's why you can't divide by zero unless you're taking limits! Because 0 does not have an inverse function!
Maybe I'll actually do graphing next time. Or maybe I'll forget until Monday morning again and write another filler post. START A BETTING POOL.
Identities! Also, zero. I'm going to explain why you can't divide by zero.
An identity is a number that, when processed through an operation with another number, gives you that other number. That sounds confusing. It isn't, really. You already know this, you just don't have a name for it.
The multiplicative identity is 1. x*1 = x, you see. It doesn't change the value of what you're multiplying it with. This is important because remember, you can write 1 as anything over itself. So 1 being an identity allows you to re-write equations and put them into a different form. Pretty cool!
The additive identity is 0, because x+0 = x. This one also lets you re-write equations. You use it constantly in simple algebra while solving for x. x+3 = 7, subtract 3 from both sides, x + 3 - 3 = 7-3; x + 0 = 4. You're using the fact that adding zero doesn't change the answer to figure out the solution to the problem.
Yeah, yeah, this is stuff you already know, but nobody sat down and bothered to explain what it meant, I'm certain. I didn't find out about identities as a THING until linear algebra, when you start using this thing called an identity MATRIX. You multiply it with a matrix and get the original matrix. UNSURPRISINGLY it's an idea that comes from more basic math concepts which are never adequately explained!
I mean, you can say it's obvious that x+0 = x, but why? Why is that obvious? Math operates on the methods we use to define it. Did you know that x0 is 1? Yeah, something times itself 0 times is equal to 1. Why? Because if it wasn't, the rest of our math wouldn't make sense. (Speaking of, the exponential identity is also 1.)
So we created this thing called an identity and defined it the way we did because it helps us solve problems.
This is only tangentially related to identities, but it's a good place to talk about zero. Why can't you divide by zero? We know from doing limits that division by zero goes to infinity. It's not finite, but the limit exists. Well, the fact that it's not finite is important. That means that x/0 doesn't actually have a value. You can't say it equals infinity, because infinity is a concept, not a number.
You can also explain it algebraically. I'll even bust out the code for this one.
Divide both sides by x, where x ≠ 0
This is true. It works.
But if you try it the other way around:
Dividing by a number is actually multiplying by the inverse, so we try multiplying by 1/0.
Unfortunately, all you get is a mess.we know is zero.
we know is infinite.
So what's
Unlike all other numbers, 0 does not have an inverse that turns it into 1. x*1/x = 1, but 0*1/0 ≠ 1 because 0/0 is not defined and it's definitely not equal to 1. And that's why you can't divide by zero unless you're taking limits! Because 0 does not have an inverse function!
Maybe I'll actually do graphing next time. Or maybe I'll forget until Monday morning again and write another filler post. START A BETTING POOL.
18 April 2011
Gosh I Hope This Post Actually Helps Somebody
Oh, gosh. It would seem that in light of my excitement over finally hitting Spring Break, I forgot to write today's post. I said we'd do graphing, right? Man, fuck graphing, listen--I don't want to write about graphing right now because I have video games to play. And while I could segue neatly from graphing to coordinate systems in games, I'm going to talk about something you can use in your daily life instead.
Let me tell you a secret, dear reader. Math isn't about numbers.
"WHA-AAAT?" you cry, as your monocle flies off, landing in your tea with a splash.
It's true. Math isn't about numbers. In fact, most of the mathematicians I know are terrible at basic arithmetic, myself included. Your college algebra professor probably sucked with numbers, no lie.
Math is about ideas. It's about problem solving. The reason your books keep throwing word problems at you is not to trip you up and confuse you--it's because when you come across applications of math in real life, you're not going to be handed an equation. You're going to be thrown a complex situation that you'll need to build your own equation from.
This isn't a post on word problems (though I am working on one). This is a post on an application of math as a problem solving tool in real life. You'll find the techniques are similar.
So what am I talking about when I say using math in real life? You know the common lament of the high school math student: "I'm never going to use any of this in real life!" High school math student, you have no imagination. There are so many ways for you to use math in real life.
The most common? Groceries. If you're shopping on a budget (and if you're a college student, you probably are), knowledge of math is vital for maximizing your dollar when you're grocery shopping.
Your total cost is the sum of all your costs. Figuring those out is pretty easy. Say you're picking up top ramen at ten cents a bag. If one bag is $.10, two bags are $.20, so on--you write that as $.10x, where x is how many bags of top ramen you're buying. The price per item times how many items. So 10 bags of top ramen would be $1.00.
If you're buying other stuff--and you should be, because a person cannot live on top ramen alone--you use the same method to figure out the cost. Price times quantity. Then you add all those products together to get the total cost of your items. If you build the equation first, you can see how many of each you can afford before throwing them in your cart and getting surprised by the cost at the end.
We all know to look for the cheapest version of a product when we're trying to save money, but here's a little-known secret--the lowest price on the shelf is not always the cheapest product. It is usually more cost effective to buy the bigger box than the smaller box.
For example, say you're picking up some frozen waffles because that's all you have time for before rushing off to that one morning class you hate. You go to your frozen foods isle and find that a box of 12 waffles costs $2, a box of 24 costs $3.50, and a big box of 36 is $5. Hopefully you are thinking "whoa wait up here," because it should be obvious that 12*3=36 but $2*3≠$5.
You can easily figure out the cost per waffle. Remember how I said the price of all your top ramen is the price times the quantity? $.10x=y, where y is your total cost. If c is your cost per item, that means your general equation is cx=y. Here, we're starting with the total cost, y=$2, and for a box of 12, our number of items x is 12, so our equation is c=$2/12, and c=~$.17. So, 17 cents per waffle for a box of 12.
A box of 36 is $5, so your total cost is y=$5 and your number of items is x=36. c=$5/36, c=~$.14. For a box of 36 waffles, the cost is 14 cents per waffle, 3 cents cheaper than for a box of 12. Thus, getting the box of 36 might be more expensive, but it is a better value. Your dollar goes farther.
You can do this for everything. Check the net weight of an item and figure out its cost per gram, or FL, or lb. Oftentimes you will find that you're throwing away money by buying the lowest-priced item on the shelf because it's the worst value per measurement.
Okay, so you know how to figure out the best value, and how to calculate your total cost. What about the sales tax, Guindo? How do I figure out that?!
First you need to know what your sales tax is. It's different in different states, obviously, but 8%~9% seems to be the average. If you want to play it safe, use 10% to calculate, and you should always end up with an end price slightly lower than you expected.
If you don't know how to calculate a percentage, it's actually pretty easy. Elementary school arithmetic tricked you into thinking it was hard. I'll do a post on percentages later I guess, but for now know that to get 10% of something, you multiply it by .10. 10% of 100 is 10, 100 times .10 is 10. (.10 is also the same as 1/10, if you find it easier to work with fractions or don't have a calculator handy.)
But finding your sum, finding 10% of it, and then adding those two together is a pain. Don't do that. There is an easier way. Think of it like this: if y is your total cost, and the sales tax is 10% of your total cost, then your final total is y + .10y. The total cost plus the sales tax. This is the same as 1y + .10y. Remember like terms from the variable post? You can add those together, and get 1.10y. So multiplying your total cost by 1.10 will give you the final total of all your items plus sales tax. Pretty neat!
So, in summary, the cost of your groceries is going to be somewhere around 1.10(price*number of items + price*number of items + price*number of items....) = final total.
Math! You do use it in real life!
Graphing next time. Maybe.
Let me tell you a secret, dear reader. Math isn't about numbers.
"WHA-AAAT?" you cry, as your monocle flies off, landing in your tea with a splash.
It's true. Math isn't about numbers. In fact, most of the mathematicians I know are terrible at basic arithmetic, myself included. Your college algebra professor probably sucked with numbers, no lie.
Math is about ideas. It's about problem solving. The reason your books keep throwing word problems at you is not to trip you up and confuse you--it's because when you come across applications of math in real life, you're not going to be handed an equation. You're going to be thrown a complex situation that you'll need to build your own equation from.
This isn't a post on word problems (though I am working on one). This is a post on an application of math as a problem solving tool in real life. You'll find the techniques are similar.
So what am I talking about when I say using math in real life? You know the common lament of the high school math student: "I'm never going to use any of this in real life!" High school math student, you have no imagination. There are so many ways for you to use math in real life.
The most common? Groceries. If you're shopping on a budget (and if you're a college student, you probably are), knowledge of math is vital for maximizing your dollar when you're grocery shopping.
Your total cost is the sum of all your costs. Figuring those out is pretty easy. Say you're picking up top ramen at ten cents a bag. If one bag is $.10, two bags are $.20, so on--you write that as $.10x, where x is how many bags of top ramen you're buying. The price per item times how many items. So 10 bags of top ramen would be $1.00.
If you're buying other stuff--and you should be, because a person cannot live on top ramen alone--you use the same method to figure out the cost. Price times quantity. Then you add all those products together to get the total cost of your items. If you build the equation first, you can see how many of each you can afford before throwing them in your cart and getting surprised by the cost at the end.
We all know to look for the cheapest version of a product when we're trying to save money, but here's a little-known secret--the lowest price on the shelf is not always the cheapest product. It is usually more cost effective to buy the bigger box than the smaller box.
For example, say you're picking up some frozen waffles because that's all you have time for before rushing off to that one morning class you hate. You go to your frozen foods isle and find that a box of 12 waffles costs $2, a box of 24 costs $3.50, and a big box of 36 is $5. Hopefully you are thinking "whoa wait up here," because it should be obvious that 12*3=36 but $2*3≠$5.
You can easily figure out the cost per waffle. Remember how I said the price of all your top ramen is the price times the quantity? $.10x=y, where y is your total cost. If c is your cost per item, that means your general equation is cx=y. Here, we're starting with the total cost, y=$2, and for a box of 12, our number of items x is 12, so our equation is c=$2/12, and c=~$.17. So, 17 cents per waffle for a box of 12.
A box of 36 is $5, so your total cost is y=$5 and your number of items is x=36. c=$5/36, c=~$.14. For a box of 36 waffles, the cost is 14 cents per waffle, 3 cents cheaper than for a box of 12. Thus, getting the box of 36 might be more expensive, but it is a better value. Your dollar goes farther.
You can do this for everything. Check the net weight of an item and figure out its cost per gram, or FL, or lb. Oftentimes you will find that you're throwing away money by buying the lowest-priced item on the shelf because it's the worst value per measurement.
Okay, so you know how to figure out the best value, and how to calculate your total cost. What about the sales tax, Guindo? How do I figure out that?!
First you need to know what your sales tax is. It's different in different states, obviously, but 8%~9% seems to be the average. If you want to play it safe, use 10% to calculate, and you should always end up with an end price slightly lower than you expected.
If you don't know how to calculate a percentage, it's actually pretty easy. Elementary school arithmetic tricked you into thinking it was hard. I'll do a post on percentages later I guess, but for now know that to get 10% of something, you multiply it by .10. 10% of 100 is 10, 100 times .10 is 10. (.10 is also the same as 1/10, if you find it easier to work with fractions or don't have a calculator handy.)
But finding your sum, finding 10% of it, and then adding those two together is a pain. Don't do that. There is an easier way. Think of it like this: if y is your total cost, and the sales tax is 10% of your total cost, then your final total is y + .10y. The total cost plus the sales tax. This is the same as 1y + .10y. Remember like terms from the variable post? You can add those together, and get 1.10y. So multiplying your total cost by 1.10 will give you the final total of all your items plus sales tax. Pretty neat!
So, in summary, the cost of your groceries is going to be somewhere around 1.10(price*number of items + price*number of items + price*number of items....) = final total.
Math! You do use it in real life!
Graphing next time. Maybe.
11 April 2011
Taking the Mystery Out of Unknowns
Some people have trouble with variables. For someone like me who's more comfortable with variables than actual numbers, that sounds pretty ridic, but it's actually not so weird. Variables are strange. Up until this point, there was nothing abstract about math at all. You had numbers and you did things with them to get other numbers. Now suddenly there's all these LETTERS and shit, what the fuck are you even supposed to do? It's not as complicated as it might seem, though. In fact, variables are pretty cool!
What is a variable? It's something that represents a number, but isn't a number. We usually use letters like x, y, or t (these are the most common ones), but we sometimes use funky symbols like θ. Don't get tripped up. The symbol being used doesn't matter, the principle of a variable is still the same. It's still just a number with an unknown or changing value. In fact, they're frequently referred to as "unknowns" when you have lots of them that you're trying to solve for.
Let's start with the basics. For equations with only one variable, you can think of the variable as a question mark. In x + 4 = 5, we don't know what x is. 4 is 4, 5 is 5, and x is ?. It's some number that makes the equation true. In this specific case, of course, it's obvious that there's only one value of x that makes the equation true. There is only ONE number that, when added to 4, equals 5, so there is only one possible value for x.
But we also have equations where there are multiple numbers that can make the equation true. For example, x2 = 4. This x is still a question mark. What number equals 4 when you square it? The obvious answer is 2. The maybe-not-so-obvious answer is -2, because squaring a real number gives you a positive result. So here, one variable can be two different numbers while still making the equation true.
There are some equations where there are an infinite number of answers that will make the equation true. Mind-blowing, I know, but this is pretty much the entire basis of algebra, here. For a trivial example, 0*x = 0 has an infinite number of possibilities for x. x can be literally anything and the equation will still be true.
For a more useful example, 2x = y has an infinite number of possibilities for x. x can be anything and y will always equal 2x. There is no value you can put in here for x that will make that untrue. In this case, we call x the independent variable, and y the dependent variable, because the value of y depends on the value of x.
You can have equations with multiple independent variables, too. x + y = z for example. x can be anything, and y can be anything, and your values for x and y don't affect each other. z, however, changes based on the values of x and y, so it is the dependent variable, while x and y are both independent variables.
Okay, Guindo, that's cool and all. But, you ask, why are variables important? Why can't we just write the numbers there? Why do we need something that represents a number but isn't one?
Lots of reasons. The biggest reason is because we don't always have static numbers to use for these things. We don't always know what x is, or we might want to be able to plug in different values for x to see what we get.
Let's say, for example, that you need to hire ninjas to kill your enemies. These ninjas charge 5 kittens a kill (they really like kittens). That means one kill costs 5 kittens, two costs 10, etc. So an equation for figuring out how many kittens you'll have to hand over to the ninjas is 5x = y, where x is how many enemies you're paying to kill, and y is how many kittens it will cost. If you need to have 5 enemies killed, you better have 25 kittens to pony up.
Or you could calculate the cost of groceries or whatever, but who cares.
The really tricky part about variables, the part most people seem to have trouble with, is that you can't treat them like numbers because you don't know what value they have. How do you know what you can and can't do with variables? Like anything else in math, we have RULES for that.
First, most important thing to keep in mind is that different letters mean different values. x is x and y is y and t is t, and you can't mix them because they all mean different things. Think of it as "apples and oranges." One variable stands for apples, the other stands for oranges, and you can't add them together.
The second thing to keep in mind is that you CAN'T divide by a variable UNLESS you know for a fact that it cannot be zero. Unless your problem says x ≠ 0, YOU CANNOT DIVIDE BY X because it might be undefined.
Here, have a handy dandy list format:
1. x + 2y cannot be simplified because they're not the same variable; don't write 3xy, it's wrong. x + 2x is 3x. This is called "adding like terms." It helps to remember that 3x means x + x + x (less abstract: 3 * 2 = 2 + 2 + 2)
2. On the other hand, you can MULTIPLY different variables together. x*y = xy. But, and this is VITAL you guys, xy terms are their own term. x + xy + y cannot be simplified. You can only add an xy term to another xy term. Same thing for exponents on variables, x2 is x*x and that's different from x.
I feel like I have droned on about variables for long enough. Hopefully that takes some of the mystery out of why we're using letters to stand in for numbers all the time.
This post was pretty boring, wasn't it? Sorry, I was having problems with laplace transforms of heaviside functions all weekend while studying for tomorrow's differential equations test. If that sounds intimidating: it is.
Next time, meh, idk. Graphs, maybe.
What is a variable? It's something that represents a number, but isn't a number. We usually use letters like x, y, or t (these are the most common ones), but we sometimes use funky symbols like θ. Don't get tripped up. The symbol being used doesn't matter, the principle of a variable is still the same. It's still just a number with an unknown or changing value. In fact, they're frequently referred to as "unknowns" when you have lots of them that you're trying to solve for.
Let's start with the basics. For equations with only one variable, you can think of the variable as a question mark. In x + 4 = 5, we don't know what x is. 4 is 4, 5 is 5, and x is ?. It's some number that makes the equation true. In this specific case, of course, it's obvious that there's only one value of x that makes the equation true. There is only ONE number that, when added to 4, equals 5, so there is only one possible value for x.
But we also have equations where there are multiple numbers that can make the equation true. For example, x2 = 4. This x is still a question mark. What number equals 4 when you square it? The obvious answer is 2. The maybe-not-so-obvious answer is -2, because squaring a real number gives you a positive result. So here, one variable can be two different numbers while still making the equation true.
There are some equations where there are an infinite number of answers that will make the equation true. Mind-blowing, I know, but this is pretty much the entire basis of algebra, here. For a trivial example, 0*x = 0 has an infinite number of possibilities for x. x can be literally anything and the equation will still be true.
For a more useful example, 2x = y has an infinite number of possibilities for x. x can be anything and y will always equal 2x. There is no value you can put in here for x that will make that untrue. In this case, we call x the independent variable, and y the dependent variable, because the value of y depends on the value of x.
You can have equations with multiple independent variables, too. x + y = z for example. x can be anything, and y can be anything, and your values for x and y don't affect each other. z, however, changes based on the values of x and y, so it is the dependent variable, while x and y are both independent variables.
Okay, Guindo, that's cool and all. But, you ask, why are variables important? Why can't we just write the numbers there? Why do we need something that represents a number but isn't one?
Lots of reasons. The biggest reason is because we don't always have static numbers to use for these things. We don't always know what x is, or we might want to be able to plug in different values for x to see what we get.
Let's say, for example, that you need to hire ninjas to kill your enemies. These ninjas charge 5 kittens a kill (they really like kittens). That means one kill costs 5 kittens, two costs 10, etc. So an equation for figuring out how many kittens you'll have to hand over to the ninjas is 5x = y, where x is how many enemies you're paying to kill, and y is how many kittens it will cost. If you need to have 5 enemies killed, you better have 25 kittens to pony up.
Or you could calculate the cost of groceries or whatever, but who cares.
The really tricky part about variables, the part most people seem to have trouble with, is that you can't treat them like numbers because you don't know what value they have. How do you know what you can and can't do with variables? Like anything else in math, we have RULES for that.
First, most important thing to keep in mind is that different letters mean different values. x is x and y is y and t is t, and you can't mix them because they all mean different things. Think of it as "apples and oranges." One variable stands for apples, the other stands for oranges, and you can't add them together.
The second thing to keep in mind is that you CAN'T divide by a variable UNLESS you know for a fact that it cannot be zero. Unless your problem says x ≠ 0, YOU CANNOT DIVIDE BY X because it might be undefined.
Here, have a handy dandy list format:
1. x + 2y cannot be simplified because they're not the same variable; don't write 3xy, it's wrong. x + 2x is 3x. This is called "adding like terms." It helps to remember that 3x means x + x + x (less abstract: 3 * 2 = 2 + 2 + 2)
2. On the other hand, you can MULTIPLY different variables together. x*y = xy. But, and this is VITAL you guys, xy terms are their own term. x + xy + y cannot be simplified. You can only add an xy term to another xy term. Same thing for exponents on variables, x2 is x*x and that's different from x.
I feel like I have droned on about variables for long enough. Hopefully that takes some of the mystery out of why we're using letters to stand in for numbers all the time.
This post was pretty boring, wasn't it? Sorry, I was having problems with laplace transforms of heaviside functions all weekend while studying for tomorrow's differential equations test. If that sounds intimidating: it is.
Next time, meh, idk. Graphs, maybe.
04 April 2011
The Root of All Math Puns
Fucking exponents, how do they work???
Actually this post is about exponents AND roots, because - get ready to have your mind blown - they are the same thing.
WHOA. BACK THE FUCK UP, GUINDO. What do you mean ROOTS and EXPONENTS are the same thing?
I proved addition and subtraction were the same fucking thing and you STILL doubt me? Sheeeeesh you people are ridic.
Okay, before we go any farther let me explain what I mean by roots and exponents. Exponents are those neat little superscripts like the 2 in x2. Roots are square roots, cube roots, and so on, that weird looking long division symbol over a number: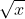
.
What an exponent means is "multiply this by itself this many times." 22 means 2*2 and 23 means 2*2*2, and so on. This is also called "power of [number]." Squares are powers of two, cubes are powers of three, etc.
A root means the opposite. What times itself this many times gets you this number?
means "what times itself three times gives you 8?" (Hint: the answer is 2.)
Roots and exponents are inverse functions. That means if you take the square root of something squared, both the root and the exponent cancel out. BUT WHY DOES THAT HAPPEN? It really isn't "because I said so," I promise.
The first thing that needs to be explained is this: a root is really a fractional exponent. That's right,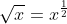
. Likewise, 
, and so on for whatever number you might put on top of that little spike (what the fuck is that thing even called anyway).
The second thing is this: when you take something with an exponent to an exponent, you multiply both exponents. When you take the square root of both sides of an equation, what you're really doing is taking both sides to a power of 1/2. So what does that mean in practice? Let's check it out.
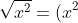^\frac{1}{2}=x^{2*\frac{1}{2}}=x^\frac{2}{2}=x^1=x "\sqrt{x^2}=(x^2)^\frac{1}{2}=x^{2*\frac{1}{2}}=x^\frac{2}{2}=x^1=x")
As you can see, the exponents end up multiplying out to become 1, which means both your root and your exponent can drop out.
You can also use this knowledge to re-write stuff into a doable form. You can't really take something to the 3/2's power without a calculator, but you can take the square root of the cube of something.
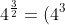^\frac{1}{2}=(64)^\frac{1}{2}=\sqrt{64}=8 "4^\frac{3}{2}=(4^3)^\frac{1}{2}=(64)^\frac{1}{2}=\sqrt{64}=8")
First you split up the exponent into ones you know how to do (a cube and a square root), and then you calculate.
Pretty cool! I think. And my opinion is the only one that matters.
>=|
BUT WAIT! THERE'S MORE!
("There's MORE? Auuuugh.")
Silence, hapless reader. There are RULES about exponents. These rules are pretty dang strict and if you break them YOUR ANSWER WILL BE WRONG FOREVER. So let's talk about exponent rules.
^2\ne x^2+y^2 "1. (x+y)^2\ne x^2+y^2")
You CAN NOT split up an added quantity with an exponent. This is not true and don't do it ever. If you have multiple terms inside a quantity taken to an exponent, you HAVE to either get rid of the exponent algebraically or expand the quantity by multiplying it out using the definition of an exponent (which is a thing you can do and I will cover it eventually).
^2=x^2*y^2 "2. (x*y)^2=x^2*y^2")
On the other hand, you CAN do this with multiplication. What this rule is really handy for is reducing roots. If you end up with, say,
, you can reduce it using this rule. Let me show you how:
^2=\frac{x^2}{y^2} "3. \left( \frac{x}{y}\right )^2=\frac{x^2}{y^2}")
Expanding on the multiplication rule, it applies to division as well. Which shouldn't surprise you because division is the same as multiplication.
} "4. x^a*x^b=x^{(a+b)}")
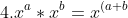If your bases are the same (and ONLY if your bases are the same, DO NOT TRY THIS IF YOUR BASES ARE DIFFERENT), then you add the exponents together. Shove the following into your calculator to confirm if you're curious:
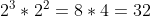
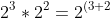}=2^5=32 "2^3*2^2=2^{(3+2)}=2^5=32")
^b=x^{ab} "5. (x^a)^b=x^{ab}")
And the one we've already discussed, if you have exponents to an exponent, then you multiply them.
But gosh, Guindo, you may ask. What about adding stuff with exponents?
Here's an unfortunate truth. You can only add stuff with exponents if that stuff has the same exponent. You cannot, CAN NOT, add x3+x2. Can't do it. On the other hand, x2+x2 CAN be added, and it is 2x2. The exponent doesn't change. You can plug in some values for x and test it out if you don't believe me.
Next time, oh, I don't know, let's talk a little bit about using letters and shit to stand in for numbers. NEXT TIME: VARIABLES!
Actually this post is about exponents AND roots, because - get ready to have your mind blown - they are the same thing.
WHOA. BACK THE FUCK UP, GUINDO. What do you mean ROOTS and EXPONENTS are the same thing?
I proved addition and subtraction were the same fucking thing and you STILL doubt me? Sheeeeesh you people are ridic.
Okay, before we go any farther let me explain what I mean by roots and exponents. Exponents are those neat little superscripts like the 2 in x2. Roots are square roots, cube roots, and so on, that weird looking long division symbol over a number:
What an exponent means is "multiply this by itself this many times." 22 means 2*2 and 23 means 2*2*2, and so on. This is also called "power of [number]." Squares are powers of two, cubes are powers of three, etc.
A root means the opposite. What times itself this many times gets you this number?
Roots and exponents are inverse functions. That means if you take the square root of something squared, both the root and the exponent cancel out. BUT WHY DOES THAT HAPPEN? It really isn't "because I said so," I promise.
The first thing that needs to be explained is this: a root is really a fractional exponent. That's right,
The second thing is this: when you take something with an exponent to an exponent, you multiply both exponents. When you take the square root of both sides of an equation, what you're really doing is taking both sides to a power of 1/2. So what does that mean in practice? Let's check it out.
As you can see, the exponents end up multiplying out to become 1, which means both your root and your exponent can drop out.
You can also use this knowledge to re-write stuff into a doable form. You can't really take something to the 3/2's power without a calculator, but you can take the square root of the cube of something.
First you split up the exponent into ones you know how to do (a cube and a square root), and then you calculate.
Pretty cool! I think. And my opinion is the only one that matters.
>=|
BUT WAIT! THERE'S MORE!
("There's MORE? Auuuugh.")
Silence, hapless reader. There are RULES about exponents. These rules are pretty dang strict and if you break them YOUR ANSWER WILL BE WRONG FOREVER. So let's talk about exponent rules.
You CAN NOT split up an added quantity with an exponent. This is not true and don't do it ever. If you have multiple terms inside a quantity taken to an exponent, you HAVE to either get rid of the exponent algebraically or expand the quantity by multiplying it out using the definition of an exponent (which is a thing you can do and I will cover it eventually).
On the other hand, you CAN do this with multiplication. What this rule is really handy for is reducing roots. If you end up with, say,
Expanding on the multiplication rule, it applies to division as well. Which shouldn't surprise you because division is the same as multiplication.
If your bases are the same (and ONLY if your bases are the same, DO NOT TRY THIS IF YOUR BASES ARE DIFFERENT), then you add the exponents together. Shove the following into your calculator to confirm if you're curious:
And the one we've already discussed, if you have exponents to an exponent, then you multiply them.
But gosh, Guindo, you may ask. What about adding stuff with exponents?
Here's an unfortunate truth. You can only add stuff with exponents if that stuff has the same exponent. You cannot, CAN NOT, add x3+x2. Can't do it. On the other hand, x2+x2 CAN be added, and it is 2x2. The exponent doesn't change. You can plug in some values for x and test it out if you don't believe me.
Next time, oh, I don't know, let's talk a little bit about using letters and shit to stand in for numbers. NEXT TIME: VARIABLES!
28 March 2011
Operations to Order
You've probably heard the acronym PEMDAS at some point in your academic career. If you haven't taken a math class since the bare minimum to graduate your last level of schooling, you've probably forgotten what it means because who even fucking uses MATH in REAL LIFE, JEEZ. (Everyone btw, you philistine.)
PEMDAS is supposed to be a mnemonic to help you remember order of operations. (If you don't know what a mnemonic is,get out bookmark dictionary.com or something.) When you see an equation, you're supposed to evaluate it in a certain order. PEMDAS is an acronym for that order:
Parentheses
Exponents
Multiplication
Division
Addition
Subtraction
Why is there a rule for this? Because if we didn't agree on the rules before we started talking about something, nobody would know what the fuck they were doing. Imagine trying to play monopoly with five different sets of house rules and everyone constantly arguing over shit the other players were doing. Eventually somebody robs the bank, the board gets flipped, and the Waterworks are on fire.
To avoid that, you lay out your agreed-upon house rules BEFORE you start playing. Math's the same way. We lay out our rules, and then we work based on them. So, PEMDAS is our rule for turn-order. Here's how it works.
PARENTHESES - first, evaluate whatever is in parentheses, starting with the innermost ones and moving to the outermost if you have multiple sets of parentheses. An operation inside parentheses is commonly referred to as a quantity. (x+2)2 is read as x plus 2 quantity squared.
EXPONENTS - next, whatever exponents are involved.
MULTIPLICATION/DIVISION - these are basically the same operation, remember? But if you're not going to the trouble of re-writing all your division as fractions (and why aren't you? It's so much easier that way), multiply first and then divide.
ADDITION/SUBTRACTION - also basically the same operation and it doesn't even require much rewriting. This comes last, after everything else has been figured out. See above examples for further examples.
Let's do an example that brings everything together.
DON'T TRIP, YOU GUYS. THIS IS GONNA LOOK REALLY FUCKING COMPLICATED.
^4)+10*3^2\div5 "2*8-3*(4\div 2+(7-3)^4)+10*3^2\div5")
What.
What did I tell you last time? Start at the top and just keep working until you get something you know how to solve. Math is all about breaking problems down and working in steps.
So let's start with the parentheses and go down through PEMDAS from there.
Click the image for a step-by-step walkthrough
[NOTE: I wrote (7-3)3 here but calculated (7-3)4. It's been changed in the equations, but the .jpg still says 3 until I get around to changing it.]
Knowing how to apply PEMDAS is vital as a basis for fucking everything else you will ever do in math.
YOU'RE WELCOME.
PEMDAS is supposed to be a mnemonic to help you remember order of operations. (If you don't know what a mnemonic is,
Parentheses
Exponents
Multiplication
Division
Addition
Subtraction
Why is there a rule for this? Because if we didn't agree on the rules before we started talking about something, nobody would know what the fuck they were doing. Imagine trying to play monopoly with five different sets of house rules and everyone constantly arguing over shit the other players were doing. Eventually somebody robs the bank, the board gets flipped, and the Waterworks are on fire.
To avoid that, you lay out your agreed-upon house rules BEFORE you start playing. Math's the same way. We lay out our rules, and then we work based on them. So, PEMDAS is our rule for turn-order. Here's how it works.
PARENTHESES - first, evaluate whatever is in parentheses, starting with the innermost ones and moving to the outermost if you have multiple sets of parentheses. An operation inside parentheses is commonly referred to as a quantity. (x+2)2 is read as x plus 2 quantity squared.
Example:
EXPONENTS - next, whatever exponents are involved.
Example:
or, if there are no parentheses to be done first:
MULTIPLICATION/DIVISION - these are basically the same operation, remember? But if you're not going to the trouble of re-writing all your division as fractions (and why aren't you? It's so much easier that way), multiply first and then divide.
Example:
ADDITION/SUBTRACTION - also basically the same operation and it doesn't even require much rewriting. This comes last, after everything else has been figured out. See above examples for further examples.
Let's do an example that brings everything together.
DON'T TRIP, YOU GUYS. THIS IS GONNA LOOK REALLY FUCKING COMPLICATED.
What.
What did I tell you last time? Start at the top and just keep working until you get something you know how to solve. Math is all about breaking problems down and working in steps.
So let's start with the parentheses and go down through PEMDAS from there.
Click the image for a step-by-step walkthrough
[NOTE: I wrote (7-3)3 here but calculated (7-3)4. It's been changed in the equations, but the .jpg still says 3 until I get around to changing it.]
Knowing how to apply PEMDAS is vital as a basis for fucking everything else you will ever do in math.
YOU'RE WELCOME.
Subscribe to:
Posts (Atom)