Alright. Let's talk about algebraic manipulation. When you're given x + 4 = 3 and told to solve for x, these are the methods you use to do it.
FIRST RULE: Whatever you do to one side of the equation, you have to do to
all sides of the equation. Otherwise you change its value.
SECOND RULE: You can multiply anything by 1. Something over itself is 1. Thus you can multiply by something over itself. (You don't have to do this on both sides because multiplying something by 1 doesn't change anything's value.)
THIRD RULE: Watch your signs. When you're squaring and square rooting, make sure you pick the correct sign for the problem.
FOURTH RULE: You can always re-write something in a different form. Division as multiplication, addition as subtraction, non-fractions as fractions, so on - as long as the new form is mathematically equivalent to the old form.
FIFTH RULE: You can always plug your variables back in to the original equation to check your work.
I'm not really going to cover examples of ALL these rules in this post - things like rule 2 are more useful when you're working with second degree polynomials and such, which is another post entirely. This post is mostly an explanation of rule 1, THE MOST IMPORTANT RULE IN MATH EVER.
Your goal is to use these rules to get a variable by itself on one side of an equals sign. Let's start with a simple example.
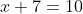
If we want to know what x is, we have to get it by itself on one side of the equals sign. We can do that by subtracting 7 from both sides. Be careful with this because it is a common misconception to think that you are MOVING that number to the other side. You're not, and if you think of it that way, you're going to get the wrong signs at some point.
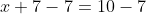

Pretty simple, right? What if it was minus 7, though? Subtracting 7 from both sides wouldn't work.
Easy enough - remember, your goal is to get the variable by itself. That means you add whatever you need to add in order to make the numbers zero.

The opposite of -7 is +7...
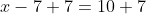
So you add 7 to both sides...

And there's your x!
It can get pretty complicated, but all you have to remember is that you want 1x on one side of the equals sign and a number on the other.

Oh man, you have to do TWO things to get x alone in this one! WHAT DO???
There's two ways to do it. Order of operations doesn't really matter - it won't change the answer, it just makes the arithmetic work out nicer sometimes. For this problem, it's just as smooth either way. I'll show you both.
First, let's get the x term (2x) by itself. We add 4 to both sides:


Now we have to turn that number in front of the x into a 1. What can you multiply 2x by to get 1x? 1/2! (Which is the same as dividing by 2.) So you divide both sides of the equation by 2:

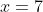
And we have our answer!
But you can divide by 2 first if you really want to - in this equation, all the terms are even, so it'll work out fine.
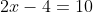
Our original equation

Divide both sides by 2
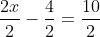
Distribute the division through each term on the left side
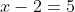
Simplify
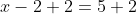
Add 2 to both sides
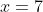
And we get the same answer!
Keep in mind that
generally you'll want to do it using the first method. You can't always guarantee the coefficient on x will divide cleanly through the other terms, so your addition afterward might get messy. Here's an example of one where you really should do your addition before your division:
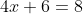
If you try to divide first you'll end up with:
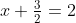
Yikes. Of course this isn't
that hard to deal with, but it's much harder to deal with than this:


In the first example, you end up having to add/subtract with fractions. In the second example, all you have to do is divide and end up with a fraction at the end (the answer is 1/2). So keep your order of operations in mind! Always do whatever leaves you with the least amount of work.
These examples are some really simple shit, I won't lie. It gets complicated.
Way complicated. What are you going to do if somebody puts this monstrosity in front of you:
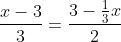
First you're going to NOT PANIC. STOP THAT. Take it one step at a time. Your first goal should always be to get rid of division by multiplying it through. When you see something like this, your first thought should be: get rid of those denominators.
We do this by cross multiplying, which is just a fancy way of saying that we multiply both sides by both denominators, but one will cancel out on each side.
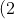(3)(\frac{x-3}{3})=(\frac{3-\tfrac{1}{3}x}{2})(2)(3))
Because this is effectively the same as:
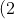(x-3)=(3-\tfrac{1}{3}x)(3))
It's easy to think of it using the shorthand of "multiply each side by the opposite side's denominator and drop the denominators from both sides." That's cross-multiplication (because you are multiplying the denominators across the equals sign).
Distribute the term through and simplify; you end up with:
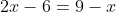
There's still an x term on both sides! DON'T TRIP. YOU'RE ALMOST THERE. Just get the x terms on the same side, and the constant terms on the other side. You do this the same way you did it before.

Add 6 to both sides to get rid of the -6 on the left
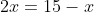
Simplify
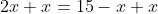
Add x to both sides to get rid of the -x on the right
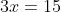
Simplify

Divide both sides by 3 to get the coefficient on x to be a 1
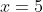
SUCCESS
These equations are like little math puzzles created solely to confound you. Don't let the extra steps fool you. You're always doing the exact same thing, every time - sometimes you're just doing more steps.
If you come across a problem you're not sure how to solve, just look for ways you can simplify the sides. Is there a denominator? Multiply it out. Are there multiple x terms? Try to get them together. Eventually you'll whittle it down to a problem you do know how to solve. The important thing is that you can't just look at a complicated problem, go, "Welp. I got nothin'," and give up. DON'T DO THAT!!! That's why people think they're bad at math. You're not bad at math, you're just bad at chipping away at a problem you think looks too hard!
Let's do one more INCREDIBLY WTF-LOOKING problem, just to show you what I mean.
^3}{x^3})
WHAT. WHAT DO I EVEN--
The exponents are the same on the top and bottom of the right side, aren't they? Everything on that side is a quantity cubed. Start there. Get rid of that by taking the cube root of both sides.
![\sqrt[3]{8}=\sqrt[3]{\frac{(4x-14)^3}{x^3}}](http://latex.codecogs.com/gif.latex?\sqrt[3]{8}=\sqrt[3]{\frac{(4x-14)^3}{x^3}})
(Protip: when you take the root of a fraction, you take the root of the top and the root of the bottom separately. Same with fractions to an exponent.)
}{x})
Now that the exponent is gone, what's your next step? Well, there's a denominator. Get rid of it. You know how to do that:
}{x}*x)

And now it looks like a standard problem that you already know how to do!
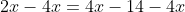
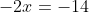
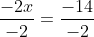
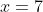
Done!
~*~ALGEBRA~*~Not as mysterious as you were maybe led to believe!
* The most important reason to make sure you really understand how this works is because it never stops being applicable. These basic algebra techniques will be with you in every math or science class you ever take.
** Likewise, the "keep chipping away at it until you get something you're familiar with" method is a lifesaver. Since this stuff will keep coming up in all your math classes forever, knowing how to start - even if you don't know where you'll end up - is vital. If you get to a point where whatever you've done has only made the problem worse, start over and try something else.